PROBLEMA 1: LOS PANELES

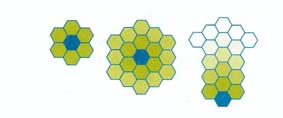
Una abeja muy atareada se acerca a ti zumbando.”Mira mi panal, crece en capas. Hay 6 hexágonos en el borde del panal más pequeña. ¿Cuántos hay en el borde del panal más grande?”

En el borde del panel más grande hay _________ hexágonos.
 

PROBLEMA 2: EL ARQUITECTO

En esta construcción nuestro arquitecto ha diseñado una serie de trazos imposibles. ¿Cuáles son?

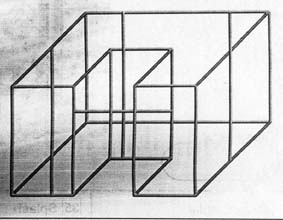
PROBLEMA 3: IGUALDADES ROMANAS

Mueve un solo palillo en cada caso para formar una igualdad con números romanos.

PROBLEMA 4: SEMIFINALES DE VOLEIBOL

Para celebrar las semifinales del Campeonato de Andalucía de Voleibol, se concentran en Sevilla los equipos representantes de cuatro provincias andaluzas distintas:
A, B, C y D.

La información que proporciona la organización es la siguiente:

1. El equipo A no viene de Sevilla ni de Córdoba.
2. El equipo B no viene de Granada ni de Cádiz.
3. Ni el equipo C ni el equipo A vienen de Cádiz.
4. El equipo B no viene de Córdoba.

Cada uno de los equipos viene de una de las cuatro provincias mencionadas. ¿Nos podríais ayudar a identificar la letra del nombre del equipo con la provincia a la que representa?

NOMBRE DEL EQUIPO:                                                                  PROVINCIA:

             A

             B

             C

             D
 

PRUEBA 1: CUADRADO MÁGICO

Toma los números del 1 al 9.
Colócalos en el cuadrado de tal forma que cada fila, cada columna y las dos diagonales sumen cada una de ellas lo mismo.
Sólo puedes utilizar una vez cada número.
 
 

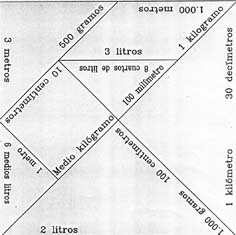
PRUEBA 2: PUZZLE DE MEDIDAS

Colocar las piezas de forma que las cantidades que se junten sean iguales.

PRUEBA 3: ESPEJOS

Coloca el espejo de manera que la figura que se vea sea:

1. Un rectángulo  2. Un triángulo  3. Un pentágono

PRUEBA 4: EL TABLERO

Añade las fichas que necesites para que haya una de cada color (ni una más, ni una menos) en todas las columnas y filas.
 
 

PRUEBA 5: TANGRAM

Utilizando todas las piezas del Tangram (ver puzzle de medidas), realizar las siguientes figuras:
 
 

PRUEBA 6: ESTIMACIÓN

1. Tomando como unidad de superficie el área de un hexágono, calcular el área de una cartulina rectangular.

2. Tomando como unidad de longitud el perímetro del hexágono, calcular el perímetro de la cartulina.
 
 

PISTA PARA PRUEBA 1: NÚMEROS

Buscamos dos números cuyos nombres escritos en castellano y en el sistema decimal, sólo difieran entre sí en una letra y en una cifra respectivamente.
¿Podríais decirnos cuáles son esos dos números?

PISTA PARA PRUEBA 2: CAZANDO RATONES

Si seis gatos cazan seis ratones en seis minutos, ¿cuántos ratones cazarán treinta gatos en treinta minutos?

PISTA PARA PRUEBA 3: ATRIBUTOS

Elena acostumbra a llevar dos, Pedro sólo una. Por lo general los hombres siempre llevan una y las mujeres dos. Aunque ahora no llevamos más de dieciocho. ¿Quién lleva más: una doctora o un electricista?

PISTA PARA PRUEBA 4: EL CUMPLEAÑOS

Un día, la tía de Claudia le preguntó:

- Hija mía, ¿cuál es la fecha de tu cumpleaños?
- Anteayer, dijo Claudia, yo tenía 19 años y el año próximo cumpliré 22.

A la tía le gustó tanto esta respuesta, que le regaló a su sobrina un coche.

¿Qué día se produce la conversación?

¿Cuándo es el cumpleaños de Claudia?

PISTA PARA PRUEBA 5: LA INFORMACIÓN NECESARIA

Se tienen cuatro tarjetas, que están pintadas de rojo o de azul por una cara, mientras en la contraria llevan una A o una B.   Las cuatro están colocadas sobre la mesa y presentan la siguiente situación:
 
 

¿A qué tarjetas es preciso dar media vuelta para poder decir con seguridad si cada tarjeta roja lleva en su dorso una A?
 

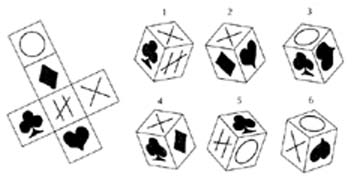
PISTA PARA PRUEBA 6: EL CUBO

Adivina cuál de los cubos es el que pertenece al desarrollo.